Model

Formula for the Model

I used a Bernoulli model with two outcomes: Yes and No, for whether the individual has one or more health conditions.

\[health\_condition_{i} \sim Bernoulli(\rho = 0.56)\]

\[\begin{equation} \begin{aligned} health\_condition_{i} = & \beta_{0} \\ + & \beta_{1} \cdot age_i \\ + & \beta_{2} \cdot sex_i \\ + & \beta_{3} \cdot marital\_status_i \\ + & \beta_{4} \cdot limited\_access_{i} \\ + & \beta_{5} \cdot num\_of\_children_{i} \\ + & \epsilon_{i} \\ \end{aligned} \end{equation}\]

Table of Coefficients

The intercept (\(\beta_{0}\)) is for calculating \(\rho\) using the average aged adult female who has never married, does not have limited access to healthcare, and has zero children.

• The more positive beta is, the greater the likelihood of having a health condition
• Likewise, more negative beta values mean a lower likelihood of having a health condition

To calculate the specific probability for a given characteristic, use the logit regression \(\rho = \frac{e ^ \beta}{1+e^\beta}\) where \(\beta\) is the characteristic’s corresponding \(\beta\) value added to the (Intercept).

Some results were expected. As age increases, the probability of having a health condition is higher. Similarly, individuals who have had difficulty accessing healthcare are more likely to also be the ones who have a chronic health condition. This relationship could potentially be mutually reinforcing.

Furthermore, divorced individuals were more likely to have a health condition. It could be that their health condition resulted in the divorce, or the divorce caused the onset of a health condition, or there was an entirely different confounding variable.

Interestingly, males, married individuals, and individuals with one to three children were less likely to have a health condition.

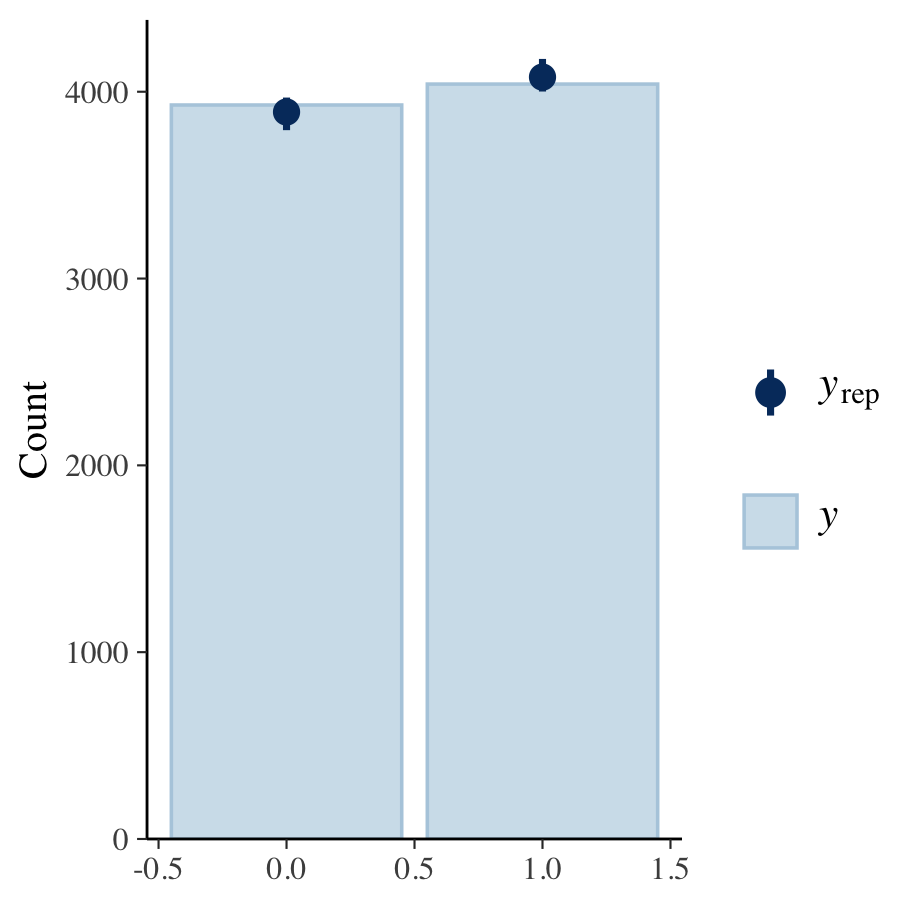
Posterior Predictive Check

Each bar represented one of the two potential outcomes for health_condition. The ten replicates had little variation between them and precisely captured the actual data.